AMETRA Research
- Innover et apporter des solutions nouvelles dans les domaines que nousa dressons,
- Monter dans l’échelle de valeurs,
- Accompagner nos clients dans leur démarche d'innovation.
projet orca
Les composites dans l’industrie

La péridynamique est une nouvelle approche prometteuse pour résoudre les problèmes impliquant des discontinuités dans la structure (fissures, fracture, fatigue…). Elle surmonte les limitations inhérentes aux modèles basés sur la mécanique classique des milieux continus dans la description de la rupture des matériaux composites. Cette nouvelle méthode de modélisation numérique a été créée par le professeur Silling {1} au début des années 2000, elle est basée sur une approche dite particulaire.
Le point fort de cette théorie est que ses équations sont valables même en présence de l’endommagent au niveau de la structure (discontinuités dans le champ de déplacement) ; de plus la ramification et la propagation des fissures peuvent être simulées de manière pratique. Alors, cette nouvelle méthode s’avère efficace quant à la détection de l’initiation de la propagation des fissures pour tous les matériaux. La défaillance du matériau peut être représentée plus réelle (figure 2) grâce à la formulation théorique détaillée dans la section suivante. Grâce à ces avantages, le nombre d’étude sur l’application de la péridynamique est en forte croissance. Dans ce contexte, Hu et al. ont développé un modèle péridynamique pour la rupture dynamique d’un composite unidirectionnel renforcés par des fibres.

Figure 2 : Propagation de fissures dans une plaque en composite comporte une pré-fissure en son centre subis une traction de 12 MPa {2}
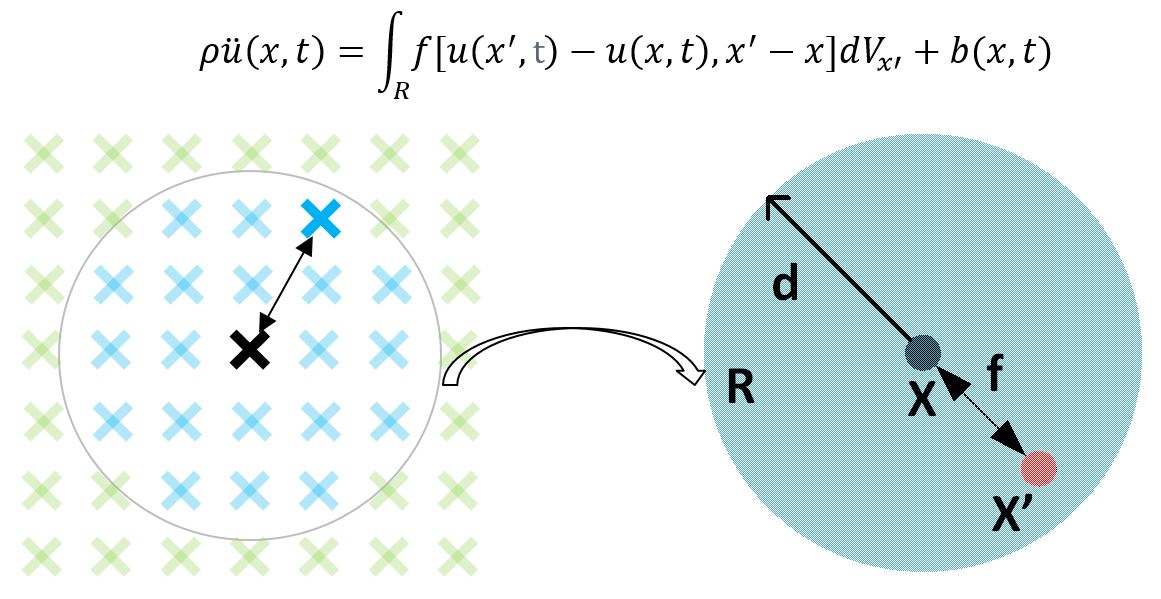
L'hypothèse principale de la péridynamique est que le corps est composé de points matériels qui sont liés à tout autre point dans une distance finie appelée horizon. Cette connexion est appelée une liaison. La notion d’horizon est une notion spécifique à la péridynamique correspondant au rayon d’influence d’une particule.
De plus, toutes les équations qui régissent le mouvement des points de la structure sont écrites dans la configuration de référence initiale et prennent la forme suivante.
Futurs travaux
Cette méthode numérique montre qu’elle est capable non seulement d'analyser divers processus de croissance de déchirures, mais aussi de prédire la charge de rupture critique et les chemins de fissures. Les voies des futurs travaux de l’équipe R&D d’Ametra Research seront consacrées à développer des modèles d’endommagement pour des structures composites et de les implémenter dans le solveur ALPS, en cours de développement par AMETRA. Le modèle sera donc validé par confrontation des résultats obtenus par ALPS avec ceux obtenus par la méthode classique FEM et par des moyens expérimentaux disponibles.
Références
{2} W. Hu, Y. D. Ha, et F. Bobaru, « Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites », Comput. Methods Appl. Mech. Eng., vol. 217‑220, p. 247‑261, avr. 2012, doi: 10.1016/j.cma.2012.01.016.